【数的処理】倍数・約数・素数 問題で使える知識を習得しよう

数的処理のこの分野の特徴は、「出題パターンが豊富」なことです。
たくさん問題を解いたはずなのに、新しい問題を解こうとすると全く解けない…という現象が頻繁に起こります。なので、この分野を苦手とする受験生がとても多いです。
これが解けるようになれば他の受験生に差をつけて合格できます！

まずは倍数・約数・素数のそれぞれをしっかり理解することから始めましょう。
参考書などの説明を理解しただけでは試験問題に対応できないので、さらに踏み込んだ、試験問題レベルの深い知識まで解説しています。
「数っておもしろい！」と思ってもらえると嬉しいです！

倍数
約数
素数
練習問題

倍数

倍数のイメージを持とう

倍数とは、「ある数を1倍、2倍、3倍…としていった数」のことです。
「…」とついているのは、15のあともさらに6倍、7倍、8倍…と永遠に続いていくからです。
例題でわかりやすく解説します。

【例題1】3の倍数を4個挙げよ。

「3の倍数」は、3という数を、1倍、2倍、3倍…としていった数なので、
3,6,9…となります。

亜子先生

倍数は無限にあるので、今回の例題は「４個挙げろ」という条件がついています。
試験問題では、必ずこの「倍数を絞り込む条件」が問題文に書かれており、正答を出すためのヒントになっています。問題文が長くて難しいと思ったら、「答えを出すためのヒントはどれかな」と意識するのがコツです。

今回は「4個だけ挙げろ」という条件なので、3を4倍までしていきます。
よって、3,6,9,12　が正解です。

【例題2】24の倍数のうち、2桁の整数を挙げよ。

無限にある倍数を絞り込むための条件はどの部分かわかりましたか？「2桁の整数」ですね。
倍数の問題を見たら、まずこの条件を探します。
そのあと、24の倍数を考えていきます。
24,48,72,96,120,144…と無限に続きますが、条件を思い出して答えを出しましょう。
24,48,72,96　が正解です。

試験問題で役立つ倍数の知識

ほとんどの参考書では、上記のような倍数の意味の解説のみで終わってしまっているのですが、残念ながらこれがわかっただけでは問題で使えません。

ここからは、問題を解く際に覚えていると役にたつ倍数の知識を解説します。
中には「そりゃそうだろ」と思うようなこともあるのですが、問題を解く段階になると意外に思いつかないことが多いです。

倍数のポイント

ある数の倍数の大きさは、その数以上となる
ある数の倍数は、すべてその数で割り切れる
隣同士の倍数の差は、必ずその数になる

1.　ある数の倍数の大きさは、その数以上となる

倍数とは、「ある数を1倍、2倍、3倍としていった数」のことなので、1倍すればその数と同じ、2倍、3倍としていけばその数より大きくなります。
【例題１】の3の倍数や【例題２】の24の倍数を見るとわかりますね。
求めた倍数は、3や24以上の数になっています。

2.　ある数の倍数は、すべてその数で割り切れる

試しに4の倍数を4つくらい挙げて、それを4で割ってみてください。すべて割り切れるはずです。

4の倍数は、4,8,12,16…　です。
全ての倍数は4で割り切れますね。

倍数とは「ある数を1から順に倍にしていった数」のことです。
逆にいえば、1倍にしたものをある数で割れば商は1、2倍したものをある数で割れば商は2、となります。

3.　隣同士の分数の差は、必ずその数になる

試しに6の倍数を3つくらい挙げて、隣同士の倍数を引き算してみてください。

6の倍数は、6,12,18,24…　です。
\(12-6=6\)
\(18-12=6\)
\(24-18=6\)

倍数は、ある数を1から順に倍にしていった数なので、
言い換えると、「その数ずつ増えていった」ことになります。
6の倍数を見ると、6に6を足して12、さらに6を足して18、さらに6を足して24、となっていますね。

最小公倍数

試験問題では、倍数の進化系「公倍数」の考え方が必要です。
公倍数とは「2つの数に共通する倍数」のことで、最小公倍数とは「公倍数のうち一番数が小さいもの」のことです。

【例題3】6と8の最小公倍数を求めよ。

基本となる求め方をまず習得しましょう。
6と8それぞれの倍数をひたすら挙げていって、一番最初に見つかった共通する数が最小公倍数です。
さらに続けていくとまた共通する数は見つかりますが、「最小」なので一番初めの数だけ答えます。

6の倍数は、6,12,18,24,30…
8の倍数は、8,16,24…
ここで24が見つかりました。
6と8の最小公倍数は24です。

【例題4】36と54の最小公倍数を求めよ。

同じようにやってみ…たいのは山々ですが、数が大きくて面倒です。
試験では、ほぼこのように大きな数が問題になるので、簡単にできる方法を教えちゃいます。

手順１
まず、割り算の筆算をひっくり返して、求めたい2つの数字を並べます。

\begin{array}{r}
\large{)}\underline{\quad36\quad54}\\
\end{array}

手順２
36と54で共通して割れる数を見つけます。
まず、偶数なので2で割れますね。
それぞれを2で割った18と27をこのように書きます。
なお、6でも割ることができます。
どんな順番で割っていっても答えは同じになるので、2のところを6にしてもOKです。

\begin{array}{r}
2\large{)}\underline{\quad36\quad54}\\
\quad18\quad27\\
\end{array}

手順３
18と27も同じように共通して割れる数を探します。
3で割れますね。

\begin{array}{r}
2\large{)}\underline{\quad36\quad54}\\
2\large{)}\underline{\quad18\quad27}\\
\quad6\phantom{0}\quad9\\
\end{array}

手順４
6と9はどちらも3で割れます。
割った答えは2と3です。
もうこれ以上共通して割れる数はないのでこれにて終了。

縦に並んだ2,3,3と、割った答えの2,3を全てかけた、
\(2\times3\times3\times2\times3=108\)が最小公倍数です。

\begin{array}{r}
2\large{)}\underline{\quad36\quad54}\\
3\large{)}\underline{\quad18\quad27}\\
3\large{)}\underline{\phantom{0}\quad6\phantom{0}\quad9}\\
\quad2\phantom{0}\quad3\\
\end{array}

【例題5】60と90と120の最小公倍数を求めよ。

3つの数字の最小公倍数の求め方もこのやり方でできます。

手順１
3つの数を並べて書きます。

\begin{array}{r}
\large{)}\underline{\quad60\quad90\quad120}\\
\end{array}

手順２
3つの数字を共通して割れる数がある限り、割っていきます。

\begin{array}{r}
2\large{)}\underline{\quad60\quad90\quad120}\\
3\large{)}\underline{\quad30\quad45\phantom{0}\quad60}\\
5\large{)}\underline{\quad10\quad15\phantom{0}\quad20}\\
\quad2\phantom{0}\quad3\phantom{0}\phantom{0}\quad4\\
\end{array}

手順３
2,3,4の3つに共通して割れる数がなくなったら、
ちょっと妥協して2つに共通して割れる数を探します。
2,4なら2で割れますね。
2で割れない3はそのまま下ろしておきます。

縦に並んだ2,3,5,2と割った答えの1,3,2をかけた、
\(2\times3\times5\times2\times1\times3\times2=360\)が最小公倍数です。

\begin{array}{r}
2\large{)}\underline{\quad60\quad90\quad120}\\
3\large{)}\underline{\quad30\quad45\phantom{0}\quad60}\\
5\large{)}\underline{\quad10\quad15\phantom{0}\quad20}\\
2\large{)}\underline{\phantom{0}\quad2\phantom{0}\quad3\phantom{0}\phantom{0}\quad4}\\
\quad1\phantom{0}\quad3\phantom{0}\phantom{0}\quad2\\
\end{array}

約数

約数のイメージを持とう

約数とは、「ある数を余りなく割り切れる数」のことです。
これも例題を見ちゃいましょう。

【例題6】8の約数をすべて挙げよ。

8の約数とは8を余りなく割り切れる数のことなので、
1,2,4,8　となります。
倍数は無限に挙げられるのに対し、約数は数によって個数が決まっています。
8の場合は4個です。

【例題7】16の約数をすべて挙げよ。

1から順番に、「16を余りなく割り切れる数」を探していきます。
1,2,4,8,16　が正解です。

試験問題で役立つ約数の知識

約数についても、いろいろなパターンの試験問題で対応できるよう、一歩踏みこんだ解説をしていきます。

約数のポイント

ある数の約数の大きさは、必ずその数以下になる
約数には必ず「1」と「その数自自身」が入っている
約数には、必ず「ペア」がいる
平方数は、約数の個数が奇数個になる

1.　ある数の約数の大きさは、必ずその数以下になる

【例題3】や【例題2】で求めた約数を見るとわかりますね。
求めた約数は、すべて8や16以下の数になっています。

2.　約数には必ず「1」と「その数自自身」が入っている

24の約数を挙げてください。
1,2,3,4,6,8,12,24　です。
次に、25の約数を挙げてください。
1,5,25　ですね。
全然違う数字のラインナップですが、1は共通していますね。
どんな数でも、必ず1では割れるので、必ず約数に入ります。
また、24の約数には24が、25の約数には25が入っています。
どんな数でも、その数だったら必ず割れて商は1になるため、約数に入ります。

3.　約数には、必ず「ペア」がいる

18の約数をすべて挙げてみてください。
1,2,3,6,9,18　ですね。正解できましたか？
このように小さい順に約数を並べ、1番左の1と1番右の18をかけると18になります。
次に、左から2番目２と、右から2番目の9もかけてみると18になります。

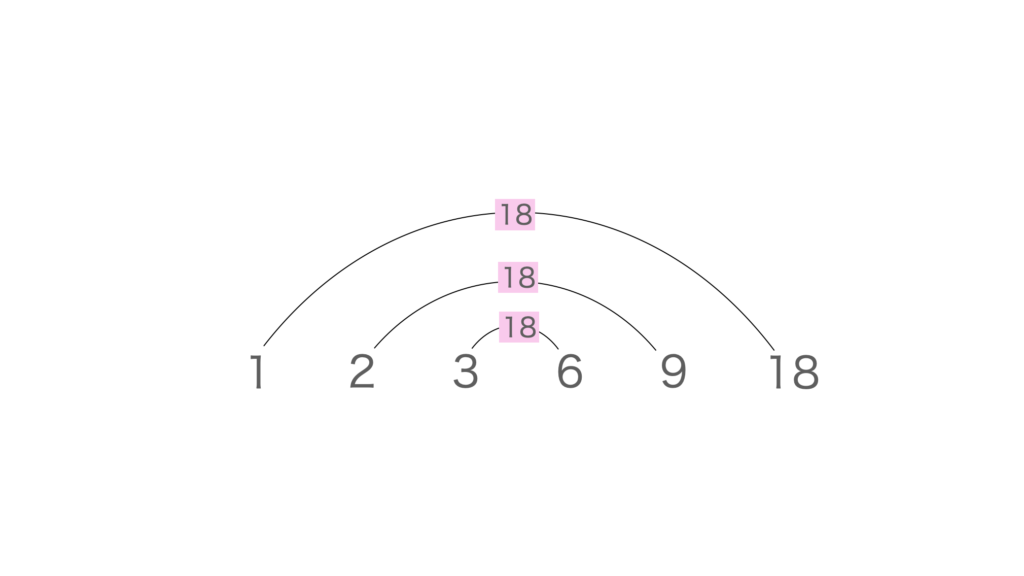
約数は、左右対称にペアがいて、ペアの2つの数字をかけると必ず同じ結果になります。
18の約数ならペア同士かけると18になり、98の約数ならペア同士かけると98になります。

4.　平方数は、約数の個数が奇数個になる

平方数とは、「ある数を2乗してできた数」のことです。
例えば、1,9,49,100　などが平方数です。
1は1を2乗した数です。9は3を、49は7を、100は10を2乗した数ですね。

試しに平方数である36の約数を挙げて考えてみます。
1,2,3,4,6,9,12,18,36　の合計9個、奇数個です。
平方数ではない数の約数（【例題３】など）は偶数個になっているはずです。確かめてみてください。

最大公約数

約数についても、進化系の「公約数」があります。
公倍数とは「2つの数に共通する約数」のことで、最大公約数とは「公約数のうち一番数が大きいもの」のことです。

「最小公約数」という言葉はありません。仮にあったとしたら、どんな数でも1になりますね。

【例題8】16と24の最大公約数を求めよ。

まずは基本のやり方。
それぞれの約数を求め、共通する約数の中で最大ものが最大公約数です。
16の約数は1,2,4,8,16
24の約数は1,2,3,4,6,8,12,24
公約数は1,2,4,8ですが、最大公約数は8です。

【例題9】210と504の最大公約数を求めよ。

来ました、数が多くて基本のやり方でやる気がしないやつ。
これも数が大きいときのやり方をご紹介します。

手順１
割り算の筆算をひっくり返して、求めたい2つの数字を並べます。

\begin{array}{r}
\large{)}\underline{\quad210\quad504}\\
\end{array}

手順２
最小公倍数のときと同様に、
210と504で共通して割れる数で割っていきます。
共通して割れるものがなくなるまで続けます。

最大公約数は、縦に並んだ数だけをかけたものが答えです。
\(2\times3\times7=42\)が最小公倍数です。

\begin{array}{r}
2\large{)}\underline{\quad210\quad504}\\
3\large{)}\underline{\quad105\quad252}\\
7\large{)}\underline{\phantom{0}\quad35\phantom{0}\quad84}\\
\phantom{0}\phantom{0}\quad5\phantom{0}\quad12\\
\end{array}

【例題10】60と90と120の最大公約数を求めよ。

【例題5】と同じ数で今度は最大公約数を求めてみます。
途中からやり方が違ってくるので、とても紛らわしいです。確実に覚えましょう！

手順１
3つの数を並べて書きます。

\begin{array}{r}
\large{)}\underline{\quad60\quad90\quad120}\\
\end{array}

手順２
3つの数字を共通して割れる数がある限り、割っていきます。
3つの数を共通して割れるのはここまでです。

最大公約数の場合は、妥協して2つで共通して割ってはいけません。
もうここで終了です。

縦に並んだ2,3,5をかけた、
\(2\times3\times5=30\)が最大公約数です。

素数

素数のイメージを持とう

素数とは、「1とその数自身の他に約数がない数」のことです。
約数のポイントのところで、

2.　約数には必ず「1」と「その数自自身」が入っている

というのがありました。

例えば4なら、約数は1,2,4　となるので、「1」と「その数自身」である4以外にも、2が約数に入っていました。
つまり4は素数ではありません。
では実際に素数にはどんな数字があるのでしょう。

2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79…

2〜79くらいまではなんとなく覚えておくと良いです。
なぜ79かというと、九九の最後が\(9\times9=81\)なので、
「九九で43ってないなあ」というように、素数かそうでないかがわかりやすいからです。

なお、素数か素数じゃないかを間違いやすそうな数字を挙げておきます。

実は素数ではないパターン
27,57：7,37,57,67　など、一の位が7となる素数が多いため、素数と間違いやすい
22,33：11が素数なので、その流れで間違いやすいが、これらは11でも割り切れる

実は素数のパターン
2：素数で唯一の偶数なので、素数のイメージがしづらい

素因数分解

試験問題で倍数・約数・素数の問題が出てきたら、高確率でこの素因数分解を使います。
問題の中でどのように使うかはまた解説するとして、
素因数分解のやり方が曖昧な方はここで完璧に使えるようにしましょう。

素因数分解とは、「ある数を素数だけの掛け算に分解すること」です。
すべての数は、素数だけの掛け算で表すことができます。
ここで、さきほど覚えた素数の羅列が役立ちます。
一番小さい素数から割っていき、最後に素数になるまで割り続けます。

【例題11】12を素因数分解せよ。

手順１
公倍数・公約数でも書いた、割り算をひっくり返したアレを準備します。
割れる素数がある限り続けていきます。

ここで注意！公倍数・公約数では割れる数ならなんでもよかったのですが、
素因数分解の場合は絶対に素数でしか割ってはいけません。
なお、素数ならどんな順番でもOKです。

\begin{array}{r}
\large{)}\underline{12}\\
\end{array}

手順２
素数を小さい順に思い出し、12を割れるかな？と考えていきます。
まず2が割れますね。
2で割った答えが6である、というのをこのように書きます。

\begin{array}{r}
2\large{)}\underline{12}\\
\phantom{0}\phantom{0}6\\
\end{array}

手順３
6はもう一回2で割れます。
割った結果は3です。
3は素数なので、もうここで終了です。
\(12=2^2\times3\) と素因数分解できます。

\begin{array}{r}
2\large{)}\underline{12}\\
2\large{)}\underline{\phantom{0}6}\\
3\\
\end{array}

【例題12】2178を素因数分解せよ。

手順１
素因数分解の筆算を書きます。

\begin{array}{r}
\large{)}\underline{2178}\\
\end{array}

手順２
数が大きくて難しいですが、偶数なので絶対に2で割れます。
（一の位が偶数ならどんな数でも偶数です。）

\begin{array}{r}
2\large{)}\underline{2178}\\
1089\\
\end{array}

手順３
もう奇数になってしまったので2では割れません。
次の素数である3では割れますね。

\begin{array}{r}
2\large{)}\underline{2178}\\
3\large{)}\underline{1089}\\
\end{array}

手順４
同じように続けていきます。
\(2178=2\times3^2\times11^2\) と素因数分解できます。

\begin{array}{r}
\phantom{0}2\large{)}\underline{2178}\\
\phantom{0}3\large{)}\underline{1089}\\
\phantom{0}3\large{)}\underline{\phantom{0}363}\\
11\large{)}\underline{\phantom{0}121}\\
11\\
\end{array}

試験問題で役立つ素数の知識

素数のポイント

2以外の偶数は素数ではない
ある数の約数は、その数を構成している素数を使って表せる

1.　2以外の偶数は素数ではない

2の約数は1,2　なので、1と自分自身しかなく、素数です。
でもその他の偶数、例えば4の約数を考えてみると、1,2,4ですね。
2以外の偶数は、1と自分自身以外にも必ず2が約数に含まれるので素数ではありません。

2.　ある数の約数は、その数を構成している素数を使って表せる

12の約数を考えてみます。1,2,3,4,6,12　です。
また、\(12=2^2\times3\) と素因数分解できますね。
12は2を2個、3を1個かけあわせて構成されていることがわかります。

約数は、これらの数字を使って表すことができます。
覚えていてほしいのは、それぞれの数字は使っても使わなくてもよく、もし使うなら持っている個数までしか使えないということです。

例えば約数の2について。
2個持っているうちの2を1個使えば表せます。3は使いません。
では約数の4はどの数字を使えば良いでしょうか。
2を2つ使えば\(2^2=4\)になりますね。
同じように、6は2を1個、3を1個使えば\(2\times3=6\)となり、持っている数字で表せました。

逆に、12の約数ではない8は持っている数字では表せません。
8を素因数分解すると\(8=2^3\)となります。
つまり、2が3個必要です。
12は2を2個しか持っていないので、8にはできません。