今までやってきた四則計算は、全て整数でした。今回は小数について解説します。小数を理解せずにいきなり計算だけを暗記しても、過去問を解く段階でつまづいてしまいます。しっかり理解しましょう。
小数とは?
小数とは0.1、2.8、9.34などのように、小数点(.)を使って表した数のことです。
この小数点より右側の数字を「小数点以下の数字」といいます。
0.1なら1、2.8なら8、9.34なら34のことですね。小数点以下の数字は、1に満たないハンパな数を表しています。

ちなみに小数点以下の数字の読み方は独特です。9.34は「きゅう てん さん よん」というように、小数点以下の数字は「さんじゅうよん」ではなくそのまま読みます。
0.1は、1を10個に分けたうちの1つなので、0.1が10個集まると1になります。
0.01は0.1を10個に分けたうちの1つなので、0.01が10個集まると0.1になります。
まずは「小数=パンパな数」というイメージを持つため、例題を見ていきましょう。
「ハンパな数」を小数で表す方法
【例題1】図のような全長が5cmの定規があります。赤いヒモの長さを「cm」だけを使って表しなさい。
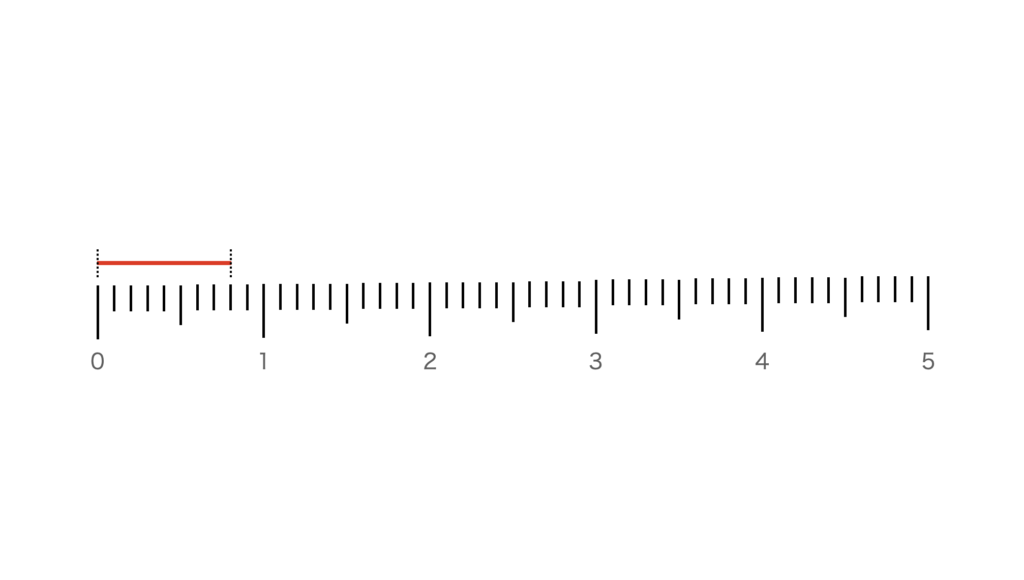
8mmのヒモ…もしこれが運命の赤い糸なら近すぎて相手に速攻で嫌われるレベルです。
1mmは1cmを10個に分けたうちの一つなので、1mm=0.1cmです。
なので、8mmを「cm」だけを使って表すと、「0.8cm」です。1cmに満たないハンパな部分が小数点以下で表されています。
【例題2】図のような全長が5cmの定規があります。青いヒモの長さを「cm」だけを使って表しなさい。
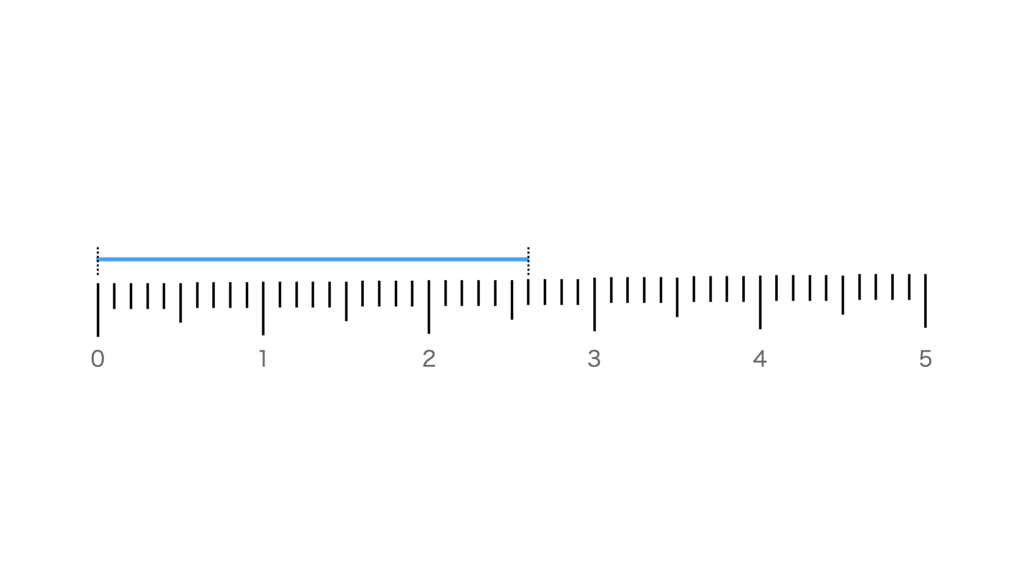
「cm」と「mm」を使って表すと、2cm6mmですね。2cmよりは大きいけど3cmには届かないハンパな部分が6mmあります。6mm=0.6cmですね。
「cm」だけを使って表すと、ハンパな部分は小数点以下になるので、「2.6cm」と表せます。
小数の大小関係
突然ですが、198と56ってどっちが大きいかわかりますか?簡単ですね。いや、少々簡単すぎたかもしれません。198ですね。整数は桁数が大きければ数は大きくなりますが、小数は異なります。
【例題3】3.5と3.7の大小関係を不等号 < を使って表しなさい。
小数点の1つ右の数字を「小数点第一位」、「\(\displaystyle\frac{1}{10}\)の位」などと呼びます。
この2つの数字は、整数(3)は共通ですが、小数点第一位の数字が違います。
3.5は、3に加えてハンパな部分が0.5だけありますね。
3.7は、3に加えてハンパな部分が0.7だけあります。大きいのは3.7ですね。
不等号を使って表すと、3.5<3.7となります。
【例題4】7.4と7.46の大小関係を不等号 < を使って表しなさい。
小数点の2つ右の数字を「小数点第二位」、「\(\displaystyle\frac{1}{100}\)の位」などと呼びます。
この2つの数字は、整数(7)と小数点第一位(4)まで共通ですね。
7.46は、7.4に加えてハンパな部分が0.06だけあるので、大きいのは7.46です。
不等号を使って表すと、7.4<7.46となります。
小数の場合は、桁数が多いからといって大きくなるわけではないので注意です。



コメント