【公務員試験】分数苦手な人はイメージを掴め！図解解説で超分かりやすく。

分数とは？と聞かれてうまく答えられますか？
分母の上に分子がある、数字を縦に並べたあの形をイメージしても、何かと聞かれると難しいのではないでしょうか。
そんな方に向けて、分数について解説します。分数を含む計算も理解しやすくなりますよ！

分数と聞いただけで電気を消して布団に潜り込みたくなる
分数の計算は何度やっても忘れてしまう
数学が苦手

こんな方はぜひこの記事で一歩前進を！

分数とは
２つの分数の大小関係
約分と通分
1. 約分
2. 通分
分数の種類
分数と割り算の関係
分数を小数に変換する
練習問題

分数とは

\(\displaystyle\frac{1}{4}\)という分数があったとしましょう。
この分数は「4個のうちの1個」という意味です。
つまり、分数は

「(分母の数)個のうちの(分子の数)個」

を表しているんですね。

では\(\displaystyle\frac{2}{5}\)を同じように説明してみましょう。
そう、「5個のうちの2個」です。

だだし、ここで注意したいのが、分母が表す「○○個のうちの」というのは、時と場合によって大きさが変わる」ということです。
わかりやすいよう、次の2つの例を考えてみます。

【例題１】お母さんが長男・次男・三男のためにケーキを３等分に切ってくれました。3人の子どもは一番大きいものを取ろうと鼻息を荒くしてその様子を見ています。さて、無事3等分に切れました。長男の取り分はどう表せますか？

3個に分けたうちの1個分なので、\(\displaystyle\frac{1}{3}\)ですね。

【例題２】今日はお母さんが奮発して長男・次男・三男のためにケーキを3つ買ってくれました！さて、一人分はどう表せますか？

3個買ってきたうちの1個なので、\(\displaystyle\frac{1}{3}\)ですね。

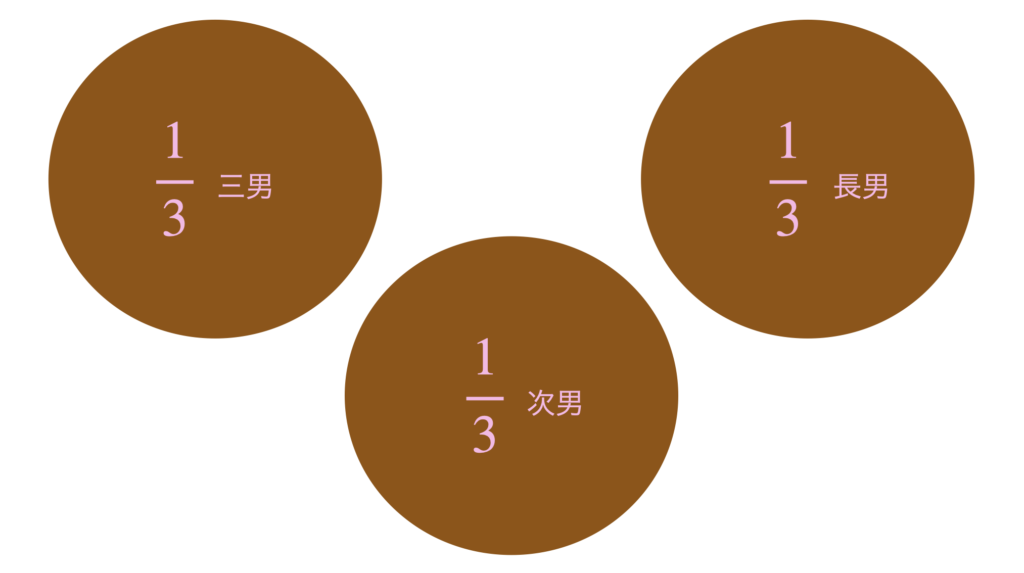
どちらも\(\displaystyle\frac{1}{3}\)と表していますが、
【例題１】の分母の3は「1個のケーキを3つに分けた」の3ですね。
一人分はそのうちの1切れなので、もしあなたがこの家の子どもなら、もっとくれよ、と思うのでは？
一方、【例題２】の分母の3は「3個あるケーキ」の3ですね。
今度は、もう一生ケーキ食べなくていいわ…と思うのではないでしょうか。

お分かりいただけただろうか…分母が同じ数字でも、その大きさは全く異なることを…
この知識は単なる計算問題では特に意識しなくてもOKですが、過去問で方程式を作るような時には必要になるので、覚えておくことをおすすめします。

２つの分数の大小関係

突然ですが、7と9はどちらが大きいですか？
簡単ですね。9です。
普通の数字なら大小関係は明確ですが、分数は単純に数字だけ見て大小の比較をすることができません。
過去問を解く段階でこれが理解できていないと全く解けなくなってしまいますので、しっかり理解しましょう。

【例題３】\(\displaystyle\frac{4}{17}\)と\(\displaystyle\frac{8}{17}\)の大小関係を不等号＜を使って表しなさい。

初めにやった「分数とは？」の答えを思い出して言葉にしてみるとわかりやすいです。
「17個のうちの4個」と「17個のうちの8個」を比べればOKですね。
難しければ図を見てみましょう。
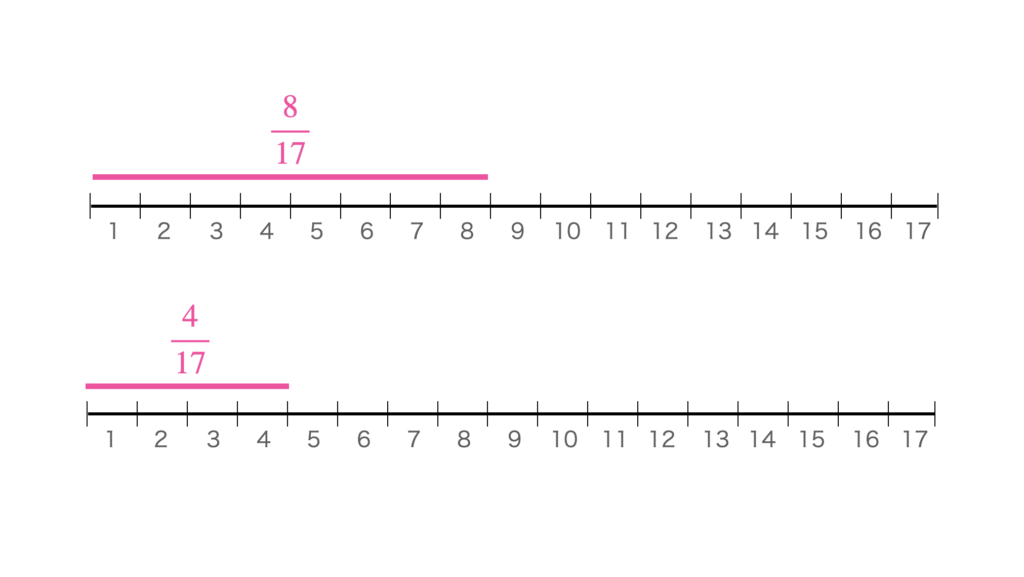
1本のヒモを17等分した図です。

\(\displaystyle\frac{8}{17}\)のほうが大きいですね。不等号を使って表すと
\(\displaystyle\frac{4}{17}<\frac{8}{17}\)です。

【例題４】\(\displaystyle\frac{1}{5}\)と\(\displaystyle\frac{1}{10}\)の大小関係を不等号＜を使って表しなさい。

これまでしっかりやってきた方はなんとなくわかるかもしれません。
言葉にしてみると、「5個のうちの1個」と「10個のうちの1個」ですね。
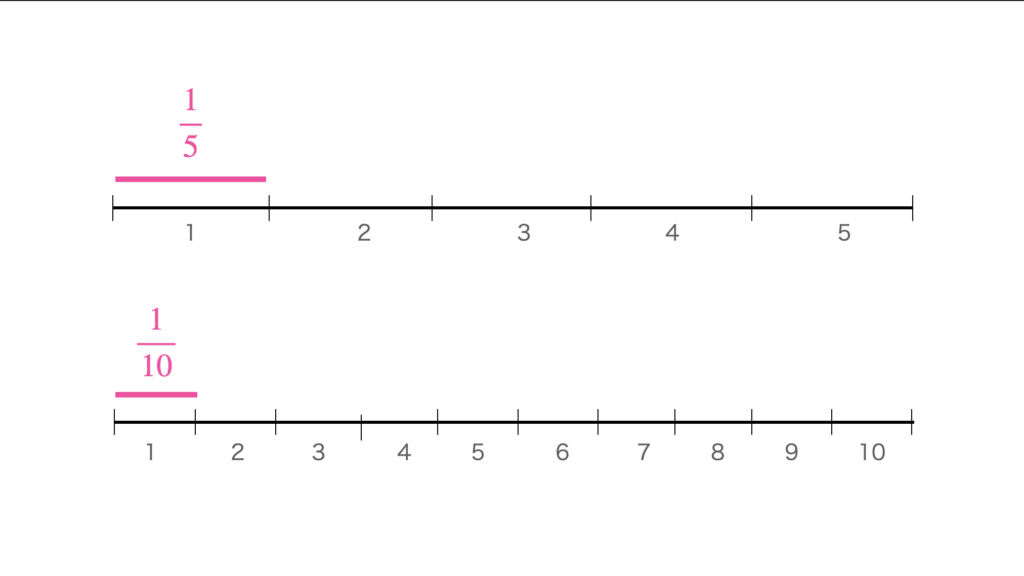
よくわからないな、という方は図をみてください。

\(\displaystyle\frac{1}{5}\)のほうが大きいので、不等号を使って表すと、
\(\displaystyle\frac{1}{10}<\frac{1}{5}\)です。
ケーキを10人で分けるより、5人で分けたほうが取り分は大きくなります。

分数の大小関係についてまとめると、

分母が同じ数のとき、分子の数が大きい分数の方が大きい
分子の数が同じとき、分母の数が小さい分数の方が大きい

となります。
これは丸暗記すると混乱するので、慣れるまで例題のヒモを思い浮かべて考えましょう。

約分と通分

次に、約分と通分を解説します。

約分

約分とは、「分数の大きさは変えずに、分母と分子の数を小さくすること」です。
分数には、「分母と分子を同じ数で割っても、分数の大きさは変わらない」という性質があります。
わかりやすいように、再度あの三兄弟に登場してもらいましょう。

【例題５】
長男・次男・三男のためにまたお母さんがケーキを切ってくれました。しかし、今日は6等分に切り、「2切れずつ食べてね」と言いました。一人分はどのように表せるでしょうか。

6個に切ったうちの2個分なので、
\(\displaystyle\frac{2}{6}\)ですね。

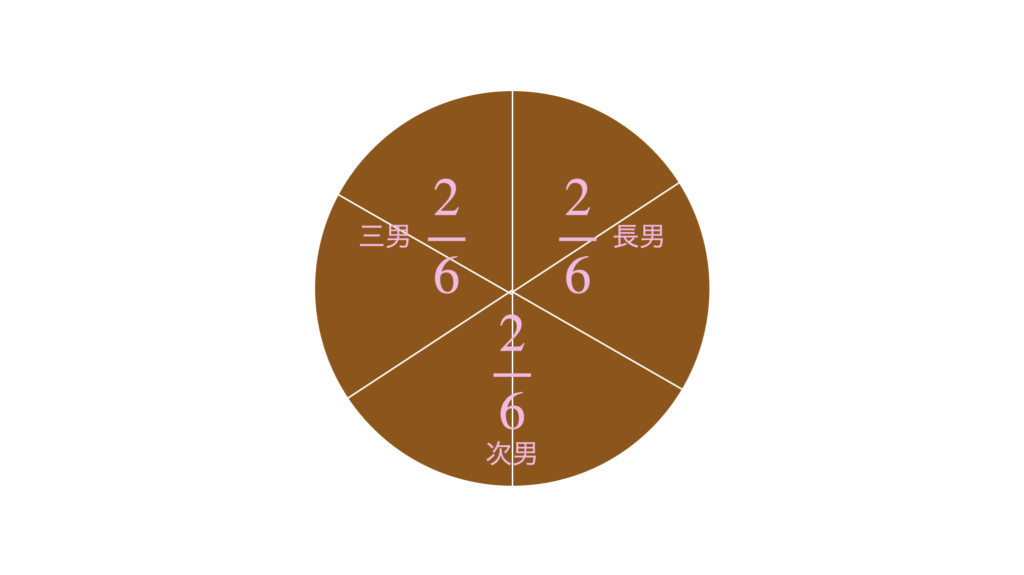
【例題１】の時のケーキと同じ大きさとして図を比べてみると、
\(\displaystyle\frac{1}{3}\)と\(\displaystyle\frac{2}{6}\)が同じ大きさなのがわかりますね。
分母の6と分子の2は、どちらも2で割ることができます。
\(\displaystyle\frac{2}{6}\)の分母と分子を2で割って\(\displaystyle\frac{1}{3}\)とすることができます。

約分をすれば、数字が小さくなるので計算がしやすくなります。分母と分子どちらも割れる数があったら積極的に約分をして、効率よく計算をしましょう。

通分

約分とよく似ている言葉ですが、
通分とは「2つの分数の分母の数を揃えること」です。
なぜそんなことが必要なのかは次の例題を見てください。

【例題６】\(\displaystyle\frac{3}{4}\)と\(\displaystyle\frac{5}{6}\)の大小関係を不等号＜を使って表しなさい。

【例題３】や【例題４】との違いはわかりますか？
【例題３】は分母が、【例題４】は分子が同じ数だったのに対し、今回は分母も分子も数が違います。
このような2つの分数の大小を比べるには、「分母の数をそろえる」、つまり通分が必要です。

手順１
4と6の共通の倍数（公倍数といいます）を見つけます。
4を2倍、3倍、4倍、としていくと
8、12、16、となりますね。
同じように6については、
12、18、24、となりますね。
今回は4を3倍、6を2倍したところで、12が同じになりました。（24を使ってもOKですが、数はなるべく小さいほうが計算が楽です）

手順２
2つの分数を、分母をその12にして書き換えます。
ここで思い出したいのが、さきほど約分でやった「分数は分母と分子を同じ数で割っても大きさは変わらない」。
割っても大きさが変わらないのであれば、「分母と分子を同じ数でかけても大きさは変わらない」ということです。

まずは\(\displaystyle\frac{3}{4}\)を、分母を12の分数に書き換えます。
分母について、4に何をかけたら12になりますか？3ですね。
今回は簡単でしたが、数が大きくなった時は\(12\div4=3\)をして求めます。
分子にも同じ数をかけないと分数の大きさが変わってしまうので、3にも3をかけます。9になりますね。
\(\displaystyle\frac{3}{4}=\frac{9}{12}\)
分母が12の分数に書き換えることができました。

次に\(\displaystyle\frac{5}{6}\)を、分母が12の分数に書き換えます。
分母について、6に2をかければ12になりますね。
分子にも同じ2をかけると10になります。
\(\displaystyle\frac{5}{6}=\frac{10}{12}\)
分母が12の分数に書き換えることができました。

これで大小の比較ができますね。
\(\displaystyle\frac{9}{12}<\displaystyle\frac{10}{12}\)　つまり　\(\displaystyle\frac{3}{4}<\displaystyle\frac{5}{6}\)です。

分数の種類

公務員試験で知っておきたいのは３種類。

真分数（しんぶんすう）
仮分数（かぶんすう）
帯分数（たいぶんすう）

言葉は覚えなくてOKですが、過去問を解けるようにするにはどんな意味か理解することは必須です。

真分数

真分数とは、分子の数字＜分母の数字　である分数のことです。今まで例題で出てきた分数は全て真分数ですね。

たとえば\(\displaystyle\frac{1}{6}\)という真分数。
1つのケーキを6個に分けたうちの1個を表しています。
真分数は、1より小さい数になります。

仮分数

仮分数とは、分母の数字＜分子の数字　である分数のことです。

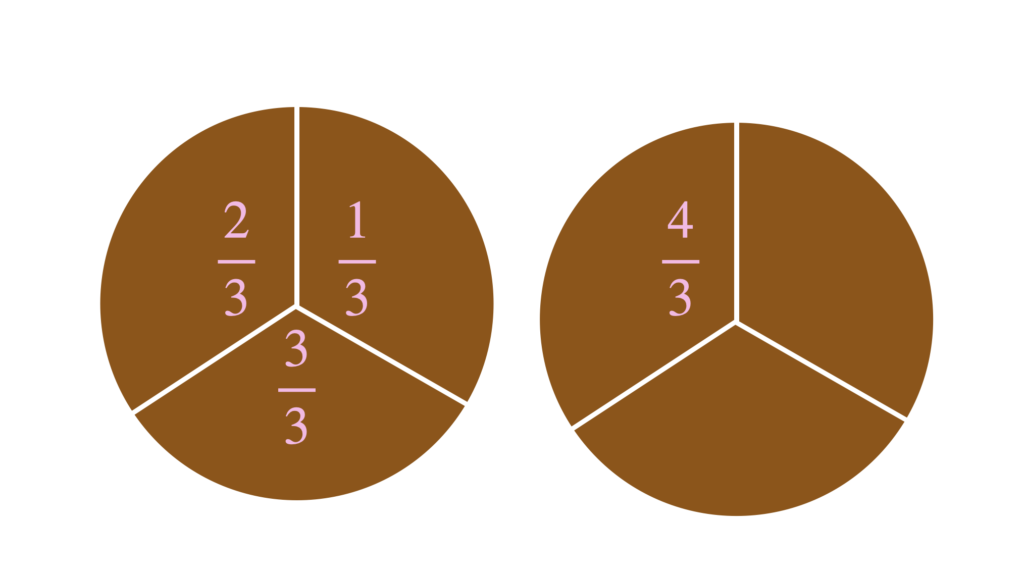
たとえば\(\displaystyle\frac{4}{3}\)という分数。少し違和感があるかもしれません。
分母が3なので、ケーキを3個に切り分けるところは今までどおりです。
でも、分子が4なので、3個に切り分けたうちの3切れ（ケーキ丸々1ホール）よりもさらに1切れ分多いですね。
図にするとこんな感じです。
仮分数は、1より大きい数になります。

帯分数

帯分数とは、仮分数を整数と分数の両方を使って表した分数です。
先ほどの\(\displaystyle\frac{4}{3}\)を帯分数で表してみます。
\(\displaystyle\frac{4}{3}\)は、ケーキ丸々1ホールとさらに\(\displaystyle\frac{1}{3}\)を合わせた数でした。それを帯分数にすると、\(\displaystyle1\frac{1}{3}\)と表せます。
1と\(\displaystyle\frac{1}{3}\)の間の＋を省略して表します。
ちなみに読み方は「いちとさんぶんのいち」です。

では、\(\displaystyle\frac{17}{5}\)を帯分数で表してみます。
数が大きくなると、図を書くのが大変ですね。計算を使ってやっちゃいます。
分母は同じ5です。
整数の部分と分子は、「17に5はいくつ入るか」を考えます。\(17\div5=3余り2\)
整数の部分には3、分子には余りの2を置きます。
\(\displaystyle\frac{17}{5}=\displaystyle3\frac{2}{5}\)

この帯分数、仮分数よりも「ケーキ1ホールと3等分のうち1切れだな」とイメージはしやすいのですが、計算では使いにくいので、帯分数を仮分数に直すやり方も覚えておくと良いです。
分母の数はそのままでOK。つまり3ですね。
分子には、「分母の数×整数の部分＋分母の数」をした数を持ってきます。つまり\(3\times1+1=4\)ですね。
\(\displaystyle1\frac{1}{3}=\frac{4}{3}\)

分数と割り算の関係

分数とはなにか、すぐ答えられるようになりましたか？「○○個のうちの○○個！」と即答できればしっかり身についています。

もうひとつ、分数は「割り算を÷の記号を使わずに表したもの」ともいうことができます。
例えばケーキを3等分して3人で分ける場合。一人分は\(\displaystyle\frac{1}{3}\)ですね。
1つのケーキを3で割るので\(1\div3\)という式になり、
\(1\div3=\displaystyle\frac{1}{3}\)と表せるのです。
「1÷3」のとき、分子から1、3　という配置になるので注意！反対にしてしまうミスがとても多いです。
今回はこの配置だけしっかり覚えておけばOKです。

分子から順番に割る！

分数を小数に変換する

小数はしっかり理解できていますか？不安な方はぜひ復習してね。

【数的処理の基本７】小数の基本を0から解説。

小数とは「１に満たないハンパな数」。小数の表し方と大小関係を図や練習問題で完璧に。小数の計算が苦手な方、方程式は解けても文章から式を作れない方はここで解決しましょう。どんな参考書、授業よりも基礎からわかりやすく解説しています。

小数→分数、分数→小数　に変換しないといけない場面が今後必ず出てきます。
どんな変換にもこれさえ覚えておけば対応できる！という最強の知識を伝授しましょう。

0.1=\(\displaystyle\frac{1}{10}\)

これを覚えておけば応用が効きます。便利っ！
ちなみに「これ、ほんとかよ？」と疑った方、そういうのとっても大事です。（疑われて悲しい、とは思いませんよ）知識をどんどん吸収して合格の実力をつけるのはあなたのような方です。

今までやってきた知識を駆使して本当かどうか確かめてみましょう。
分数は「分子の数÷分母の数」でした。また、小数の割り算を思い出します。

\begin{array}{l}
&\frac{1}{10}\\
=&1\div10\\
=&0.1
\end{array}

証明できましたね。覚えてしまうと楽です。