「割合」って?
SPIや数的処理に苦手意識を持つ人は、もう100%全員必ず!割合の基礎が抜けています。
でももう大丈夫!割合の基礎をマスターできるはずです。
まずは計算しなくても分かりやすい例で考えてみます。
【例題1】30人のクラスの15人が男子である。男子の割合は何%か。
なんとなく感覚で分かるのではないでしょうか。そう、クラスの半分の50%です。
割合とは、「ある基準に対して、どれだけの量かを表す比率」を表すものです。
では、試験レベルの問題を目指して順を追って説明していきます。
「数」と「割合」の違い
こんな場面を考えてみます。

ねーねー、Bちゃんのクラスって男子何人?

15人。

まじかー!バレンタイン大変だね。あたしんとこは8人だから楽だわー。
Aちゃんは男子の人数が知りたいのですね。
もしこのとき、 男子の人数を聞かれたBちゃんが「男子は50%だよ」などと答えていたらどうでしょう。
Aちゃんは「え?クラス何人のうちの50%?」となってしまい、結局チョコをいくつ用意するのか分かりません。
次にこんな場面を考えます。

うちの学校、男子マジ少ないわー。

どんくらいなの?

10%くらいかな。
今回Aちゃんはクラス全体を基準として、男子の割合がどのくらいかを知りたいようです。
もしここでBちゃんが「15人」と答えていたらどうでしょう。
クラス全体の人数がわからないのに、「15人」が多いのか少ないのかわかりません。クラスが40人に対して男子15人なら、Bちゃんは「男子少ない」と思うし、クラスが20人に対して男子が15人なら「男子多い」と思うでしょう。
でも、10%という割合を使うことにより、クラス全体の人数が分からなくても男子が少ないことを伝えることができます。
数 人数、個数、値段など、物の量を表す。単位がつく。
割合 基準となる量に対してどのくらいの割合かを表す。
割合の3つの表し方
%を使って表してきた割合ですが、小数や分数で表すこともできます。
次の変換表は暗記必須!そして思い出さなくてもすらすら頭の中で変換できる必要があります。
男子の割合10%は、小数では0.1、分数では\(\displaystyle\frac{1}{10}\)となります。
この表をもとに、数字が変わってもしっかり変換できるようにしましょう。
| パーセント | 1% | 10% | 100% |
| 小数 | 0.01 | 0.1 | 1 |
| 分数 | \(\displaystyle\frac{1}{100}\) | \(\displaystyle\frac{1}{10}\) | 1 |
割合の求め方
冒頭の例を計算で求めてみます。
こんな手順を踏んでいけば簡単です。
- 「割合を求めたい量」と「基準となる量」を見つける
- 公式に当てはめて計算
\(割合=割合を求めたい量\div基準となる量\)
【例題1】30人のクラスの15人が男子である。男子の割合は何%か。
1.「割合を求めたい量」と「基準となる量」を見つけます。
「割合を求めたい量」の方がわかりやすいので、必ずこちらから見つけましょう。
今回は男子の割合を知りたいので、
割合を求めたい量=15 です。
次に、「基準となる量」を見つけます。
クラス全体の人数を基準としているので、
基準となる量=30 です。
そして、2.公式に当てはめていきましょう。
\(15\div30=0.5\)
計算をすると小数で出ました。
あの変換表を思い出すと、0.5=50% と分かります。
さてさて、小数の記事で、「分数と割り算の関係」を紹介したのを覚えていますか?
この知識を使って分数で出しても答えは必ず同じになります。
\begin{array}{l}
&15\div30\\
=&\displaystyle\frac{15}{30}\\
=&\displaystyle\frac{1}{2}\\
\end{array}
\begin{array}{l}
&\displaystyle\frac{1}{2}\\
=&1\div2\\
=&0.5\\
\end{array}
割合の色々な計算
割合の公式 \(割合=割合を求めたい量\div基準となる量\) を応用すると実にさまざまな計算ができるようになります。そして、その計算がまさに数的処理やSPI3の問題なのです。
例題1 は割合を求める問題でしたが、クラスの人数や男子の人数を答えさせる問題もあります。
そんな時でも使えるのが、この図。
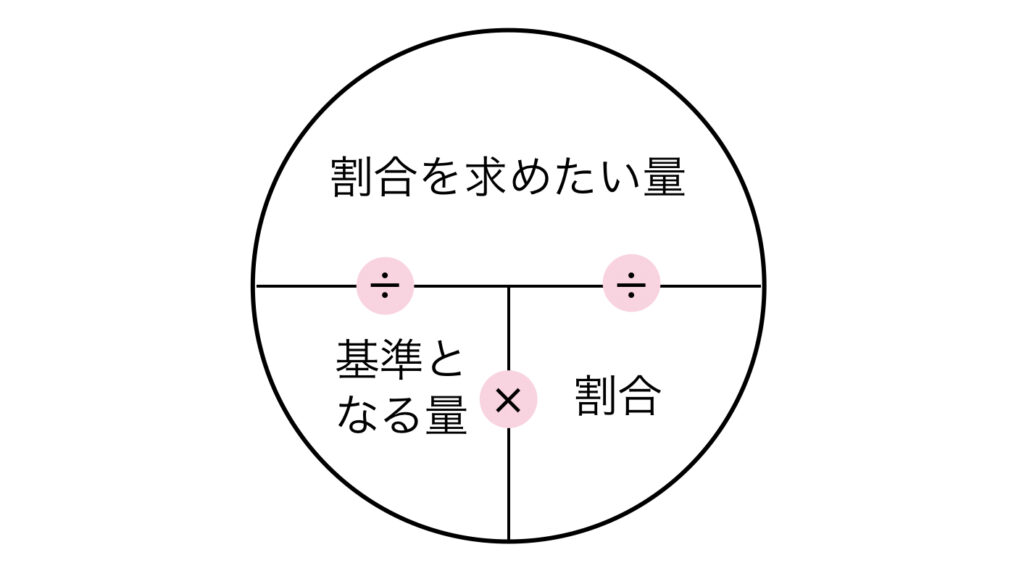
まるを描いたらその中にアルファベットの「T」を書きます。
上から反時計回りに「求めたい量」→「基準となる量」→「割合」と書き入れます。
この順番は絶対に守って!「もっと極めて」と覚えましょう。
そしてこの表の使い方。「T」と描いた横棒は\(\div\)、縦棒は\(\times\) です。
一つ注意なのは、割合は必ず%ではなく、小数か分数を使うこと!
この使い勝手の良さを体験してください。
【例題2】50人のクラスの男子の割合は30%である。男子は何人か。
割合の問題だ!とわかったらまず もっと極めての図を書きます。
覚えるためにも必ず自分で書いてみてね!
そして、今回求めたいのは3つのうちどれかな?と考えます。
割合の求め方でやった2ステップを思い出します。クラス全体の人数を基準にして男子の人数を知りたいので、「割合を求めたい量」を求めたいのですね。
上にある「割合を求めたい量」を指か何かで隠します。そして残ったものを計算します。
\begin{array}{l}
&基準となる量\times割合\\
=&50\times0.3\\
=&15\\
\end{array}
男子は15人と分かりました。
【例題3】あるクラスには42人の女子がいて、割合は70%である。クラス全体の人数は何人か。
今回求めるのは、「基準となる量」です。それを指で隠すと、残りの計算は…
\begin{array}{l}
&割合を求めたい量\div割合\\
=&42\times0.7\\
=&60\\
\end{array}
このクラスは60人の大所帯だったようです。
練習問題
割合についてイメージが持てて、少し苦手意識が薄れたのではないでしょうか。
練習問題でさらに自分のものにしていきましょう。



